Física

Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.

En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio central (como el de La Tierra), el movimiento es elíptico. En la superficie de la Tierra, ese movimiento es tan parecido a una parábola que perfectamente podemos calcular su trayectoria usando la ecuación matemática de una parábola. La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al aire, la piedra intenta realizar una elipse en uno de cuyos focos está el centro de la Tierra. Al realizar esta elipse inmediatamente choca con el suelo y la piedra se para, pero su trayectoria es en realidad un "trozo" de elipse. Es cierto que ese "trozo" de elipse es casi idéntico a un "trozo" de parábola. Por ello utilizamos la ecuación de una parábola y lo llamamos "tiro parabólico". Si nos alejamos de la superficie de la Tierra sí tendríamos que utilizar una elipse(como en el caso de los satélites artificiales).

El movimiento parabólico puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.

El tiro parabólico tiene las siguientes características:

Tipos de movimiento parabólico

El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.Movimiento parabólico (completo)

1. Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
2. La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
3. Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.
4. El tiempo que tarda en alcanzar su altura máxima es el mismo tiempo que tarda en recorrer la mitad de su distancia horizontal, es decir, el tiempo total necesario para alcanzar la altura máxima y regresar al suelo es el mismo para el total de recorrido horizontal.

PRIMERA LEY DE NEWTON

Esta indica que si un cuerpo dado no está sujeto a la acción de fuerzas, mantendrá sin cambio su velocidad (en magnitud y dirección). Esta propuesta se le debe originalmente a Galileo, pero Newton la adoptó como la primera de sus leyes para describir el movimiento de cuerpos.

Inercia

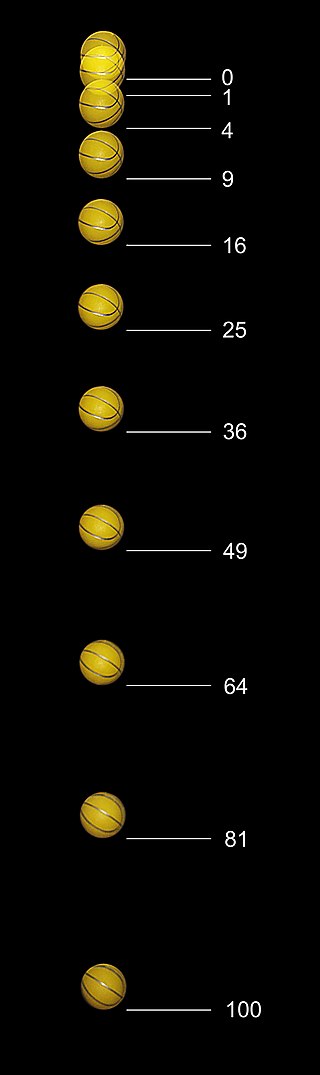
La caída libre como sistema de referencia

Un sistema de referencia ligado a un cuerpo en caída libre puede considerarse inercial o no inercial en función del marco teórico que se esté usando.

En la física clásica, la fuerza gravitatoria que se ejerce sobre una masa es proporcional a la intensidad del campo gravitatorio en la posición espacial donde se encuentre dicha masa. La constante de proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como establece el principio de equivalencia. En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica. Por tanto, desde el punto de vista de la física clásica, un sistema de referencia en caída libre es un sistema acelerado por la fuerza de la gravedad y, como tal, es no inercial. Por el contrario, desde el punto de vista de la física relativista, el mismo sistema de referencia es inercial, pues aunque está acelerado en el espacio, no está acelerado en el espacio-tiempo. La diferencia radica en la propia definición de los conceptos geométricos y cinemáticos, que para cada marco teórico son completamente diferentes.Caída libre ideal
Véase también: Ecuaciones para un cuerpo en caída libre


En la caída libre ideal, se desprecia la resistencia aerodinámica que presenta el aire al movimiento del cuerpo, analizando lo que pasaría en el vacío. En esas condiciones, la aceleración que adquiriría el cuerpo sería debida exclusivamente a la gravedad, siendo independiente de su masa; por ejemplo, si dejáramos caer una bala de cañón y una pluma en el vacío, ambos adquirirían la misma aceleración, , que es la aceleración de la gravedad
Ecuación del movimiento

De acuerdo a la segunda ley de Newton, la fuerza que actúa sobre un cuerpo es igual al producto de su masa por la aceleración que adquiere. En caída libre sólo intervienen el peso (vertical, hacia abajo) y el rozamiento aerodinámico 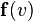en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:




La aceleración de la gravedad lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.

Para otros usos de este término, véase Vector (desambiguación).
Este artículo trata sobre el concepto físico de vector. Para el tratamiento matemático formal, véase Espacio vectorial.

En Matemáticas se define un vector como un elemento de un espacio vectorial. Esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo, la longitud y la orientación. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo. Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta dirigidos («flechas») en el plano o en el espacio .En física, un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida por un punto del espacio donde se mide dicha magnitud, además de un módulo (o longitud), su dirección (u orientación) y su sentido (que distingue el origen del extremo).

Algunos ejemplos de magnitudes físicas que son magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan sólo por su módulo (lo que marca el velocímetro, en el caso de un automóvil), sino que se requiere indicar la dirección y el sentido (hacia donde se dirige); la fuerza que actúa sobre un objeto, ya que su efecto depende, además de su intensidad o módulo, de la dirección en la que actúa; también, el desplazamiento de un objeto.

Esta sección explica los aspectos básicos, la necesidad de los vectores para representar ciertas magnitudes físicas, los componentes de un vector, la notación de los mismos, etc.

Se llama vector de dimensión  a una tupla de  números reales (que se llaman componentes del vector). El conjunto de todos los vectores dedimensión  se representa como  (formado mediante el producto cartesiano).

Así, un vector  perteneciente a un espacio  se representa como:

, donde 

Un vector también se puede ver desde el punto de vista de la geometría como vector geométrico (usando frecuentemente el espacio tridimensional  ó bidimensional ).

Un vector fijo del plano euclídeo es un segmento orientado, en el que hay que distinguir tres características:^1 2 3

En inglés, la palabra "direction" indica tanto la dirección como el sentido del vector, con lo que se define el vector con solo dos características: módulo y dirección.⁴

Los vectores fijos del plano se denotan con dos letras mayúsculas, por ejemplo , que indican su origen y extremo respectivamente.

Un vector se puede definir por sus coordenadas, si el vector esta en el plano xy, se representa:

siendo sus coordenadas:

Siendo el vector la suma vectorial de sus coordenadas:

Si un vector es de tres dimensiones reales, representado sobre los ejes x, y, z, se puede representar:

siendo sus coordenadas:

Si representamos el vector gráficamente podemos diferenciar la recta soporte o dirección, sobre la que se traza el vector.

El módulo o amplitud con una longitud proporcional al valor del vector.

El sentido, indicado por la punta de flecha, siendo uno de los dos posibles sobre la recta soporte.

El punto de aplicación que corresponde al lugar geométrico al cual corresponde la característica vectorial representado por el vector.

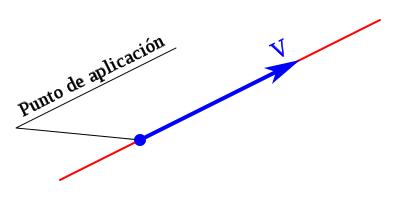
El nombre o denominación es la letra, signo o secuencia de signos que define al vector.

Por lo tanto en un vector podemos diferenciar: